0CTF/TCTF 2019 Quals Crypto

babyrsa

此题为有限域上不可约多项式的RSA，详情就看一下链接：

https://wenku.baidu.com/view/038968b632d4b14e852458fb770bf78a65293a37.html

解题分为四个步骤：

factor n，得到p、q
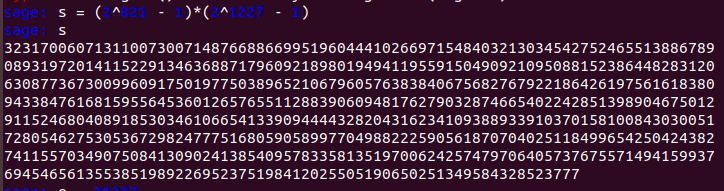
求s = (2 ^ 821 - 1) * (2 ^ 1227 - 1)
计算d，d = modinv(e,s)
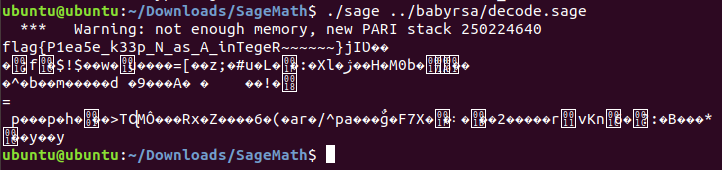
getflag，flag = pow(cipher, d, n)

第一步：

1
2
3

sage: P=PolynomialRing(GF(2),'x')
sage: n = xxxx
sage: n.factor()

可以得到

1
2

p = x^821 + x^820 + x^819 + x^818 + x^817 + x^814 + x^813 + x^812 + x^810 + x^808 + x^807 + x^804 + x^801 + x^796 + x^795 + x^794 + x^790 + x^787 + x^786 + x^784 + x^781 + x^780 + x^779 + x^778 + x^777 + x^776 + x^775 + x^774 + x^773 + x^771 + x^770 + x^768 + x^766 + x^762 + x^761 + x^760 + x^758 + x^757 + x^752 + x^749 + x^748 + x^747 + x^740 + x^737 + x^736 + x^732 + x^727 + x^723 + x^722 + x^719 + x^718 + x^717 + x^716 + x^715 + x^714 + x^711 + x^710 + x^708 + x^704 + x^703 + x^702 + x^701 + x^700 + x^699 + x^698 + x^696 + x^692 + x^690 + x^689 + x^687 + x^685 + x^683 + x^681 + x^676 + x^674 + x^672 + x^671 + x^670 + x^668 + x^667 + x^665 + x^664 + x^663 + x^661 + x^660 + x^659 + x^657 + x^656 + x^655 + x^651 + x^649 + x^646 + x^644 + x^637 + x^636 + x^634 + x^633 + x^632 + x^631 + x^628 + x^626 + x^625 + x^622 + x^621 + x^620 + x^614 + x^611 + x^609 + x^608 + x^605 + x^604 + x^599 + x^597 + x^592 + x^591 + x^589 + x^580 + x^578 + x^574 + x^572 + x^569 + x^566 + x^565 + x^563 + x^562 + x^560 + x^552 + x^550 + x^545 + x^544 + x^543 + x^542 + x^540 + x^538 + x^537 + x^534 + x^533 + x^528 + x^527 + x^526 + x^523 + x^522 + x^519 + x^518 + x^515 + x^514 + x^512 + x^505 + x^503 + x^502 + x^500 + x^498 + x^496 + x^493 + x^492 + x^491 + x^490 + x^489 + x^487 + x^482 + x^480 + x^479 + x^478 + x^476 + x^474 + x^472 + x^471 + x^470 + x^469 + x^468 + x^466 + x^462 + x^459 + x^458 + x^457 + x^456 + x^454 + x^453 + x^451 + x^449 + x^447 + x^445 + x^443 + x^442 + x^441 + x^440 + x^437 + x^434 + x^428 + x^425 + x^424 + x^423 + x^420 + x^415 + x^412 + x^411 + x^410 + x^408 + x^405 + x^404 + x^403 + x^401 + x^400 + x^394 + x^391 + x^390 + x^389 + x^388 + x^384 + x^383 + x^382 + x^379 + x^378 + x^376 + x^375 + x^372 + x^371 + x^370 + x^368 + x^366 + x^365 + x^364 + x^361 + x^358 + x^357 + x^356 + x^354 + x^351 + x^347 + x^345 + x^344 + x^340 + x^339 + x^335 + x^334 + x^333 + x^332 + x^331 + x^328 + x^326 + x^322 + x^318 + x^315 + x^312 + x^306 + x^303 + x^302 + x^301 + x^300 + x^299 + x^298 + x^297 + x^295 + x^293 + x^291 + x^289 + x^288 + x^287 + x^286 + x^285 + x^282 + x^280 + x^279 + x^277 + x^274 + x^273 + x^270 + x^269 + x^268 + x^263 + x^262 + x^261 + x^259 + x^258 + x^257 + x^256 + x^252 + x^250 + x^249 + x^245 + x^244 + x^243 + x^242 + x^236 + x^234 + x^233 + x^232 + x^228 + x^225 + x^223 + x^222 + x^221 + x^219 + x^218 + x^215 + x^214 + x^213 + x^211 + x^210 + x^209 + x^207 + x^205 + x^203 + x^202 + x^200 + x^198 + x^197 + x^193 + x^191 + x^190 + x^185 + x^184 + x^182 + x^180 + x^179 + x^177 + x^172 + x^168 + x^167 + x^165 + x^163 + x^161 + x^159 + x^157 + x^156 + x^155 + x^154 + x^153 + x^151 + x^150 + x^149 + x^148 + x^146 + x^145 + x^143 + x^139 + x^137 + x^136 + x^135 + x^133 + x^132 + x^130 + x^127 + x^126 + x^125 + x^124 + x^122 + x^121 + x^120 + x^119 + x^117 + x^116 + x^113 + x^111 + x^110 + x^109 + x^108 + x^107 + x^106 + x^105 + x^100 + x^97 + x^95 + x^89 + x^88 + x^87 + x^86 + x^85 + x^84 + x^82 + x^81 + x^80 + x^77 + x^76 + x^75 + x^74 + x^69 + x^67 + x^65 + x^61 + x^59 + x^57 + x^53 + x^52 + x^50 + x^49 + x^48 + x^45 + x^41 + x^40 + x^36 + x^34 + x^33 + x^27 + x^26 + x^24 + x^23 + x^22 + x^21 + x^20 + x^19 + x^18 + x^15 + x^14 + x^12 + x^9 + x^6 + x^4 + x^3 + x + 1
q = x^1227 + x^1226 + x^1225 + x^1224 + x^1219 + x^1214 + x^1213 + x^1211 + x^1210 + x^1208 + x^1205 + x^1203 + x^1202 + x^1201 + x^1198 + x^1197 + x^1194 + x^1193 + x^1188 + x^1185 + x^1184 + x^1183 + x^1180 + x^1178 + x^1177 + x^1175 + x^1173 + x^1171 + x^1170 + x^1169 + x^1168 + x^1166 + x^1164 + x^1163 + x^1162 + x^1160 + x^1157 + x^1155 + x^1151 + x^1149 + x^1144 + x^1143 + x^1142 + x^1141 + x^1140 + x^1139 + x^1137 + x^1136 + x^1135 + x^1134 + x^1130 + x^1126 + x^1122 + x^1121 + x^1120 + x^1118 + x^1117 + x^1115 + x^1114 + x^1111 + x^1110 + x^1108 + x^1107 + x^1105 + x^1104 + x^1103 + x^1102 + x^1101 + x^1099 + x^1094 + x^1092 + x^1090 + x^1089 + x^1085 + x^1082 + x^1079 + x^1075 + x^1074 + x^1073 + x^1070 + x^1068 + x^1067 + x^1066 + x^1065 + x^1064 + x^1061 + x^1060 + x^1059 + x^1058 + x^1055 + x^1054 + x^1053 + x^1051 + x^1047 + x^1046 + x^1043 + x^1042 + x^1041 + x^1039 + x^1037 + x^1035 + x^1034 + x^1033 + x^1031 + x^1029 + x^1028 + x^1027 + x^1026 + x^1025 + x^1023 + x^1021 + x^1019 + x^1018 + x^1016 + x^1014 + x^1012 + x^1009 + x^1006 + x^1004 + x^1002 + x^1000 + x^999 + x^996 + x^994 + x^993 + x^992 + x^991 + x^990 + x^989 + x^988 + x^984 + x^981 + x^980 + x^978 + x^977 + x^976 + x^974 + x^972 + x^967 + x^965 + x^964 + x^963 + x^962 + x^958 + x^957 + x^955 + x^953 + x^952 + x^951 + x^950 + x^949 + x^948 + x^947 + x^945 + x^944 + x^939 + x^936 + x^935 + x^934 + x^931 + x^930 + x^926 + x^924 + x^923 + x^920 + x^917 + x^913 + x^912 + x^910 + x^909 + x^908 + x^907 + x^906 + x^905 + x^903 + x^902 + x^901 + x^899 + x^896 + x^893 + x^892 + x^891 + x^887 + x^886 + x^885 + x^884 + x^883 + x^880 + x^877 + x^876 + x^872 + x^868 + x^867 + x^864 + x^863 + x^862 + x^861 + x^858 + x^856 + x^855 + x^854 + x^851 + x^847 + x^846 + x^844 + x^843 + x^842 + x^841 + x^840 + x^838 + x^836 + x^835 + x^833 + x^832 + x^830 + x^829 + x^828 + x^826 + x^825 + x^822 + x^821 + x^817 + x^815 + x^812 + x^811 + x^810 + x^808 + x^806 + x^804 + x^803 + x^802 + x^801 + x^800 + x^797 + x^792 + x^790 + x^789 + x^788 + x^787 + x^785 + x^784 + x^783 + x^781 + x^780 + x^778 + x^777 + x^776 + x^774 + x^771 + x^770 + x^769 + x^766 + x^764 + x^762 + x^759 + x^755 + x^751 + x^749 + x^748 + x^747 + x^746 + x^742 + x^737 + x^734 + x^733 + x^729 + x^727 + x^725 + x^724 + x^723 + x^722 + x^720 + x^718 + x^715 + x^713 + x^711 + x^709 + x^707 + x^706 + x^702 + x^699 + x^698 + x^695 + x^692 + x^687 + x^680 + x^679 + x^678 + x^677 + x^676 + x^674 + x^670 + x^669 + x^668 + x^662 + x^656 + x^654 + x^653 + x^652 + x^651 + x^648 + x^646 + x^645 + x^644 + x^642 + x^640 + x^639 + x^638 + x^637 + x^634 + x^633 + x^632 + x^629 + x^628 + x^627 + x^626 + x^625 + x^623 + x^619 + x^617 + x^613 + x^612 + x^611 + x^610 + x^605 + x^604 + x^603 + x^601 + x^597 + x^595 + x^593 + x^591 + x^590 + x^589 + x^588 + x^587 + x^585 + x^583 + x^581 + x^580 + x^577 + x^576 + x^574 + x^573 + x^572 + x^570 + x^569 + x^563 + x^557 + x^555 + x^553 + x^551 + x^548 + x^546 + x^545 + x^541 + x^538 + x^535 + x^534 + x^529 + x^528 + x^527 + x^526 + x^525 + x^524 + x^523 + x^522 + x^521 + x^520 + x^519 + x^518 + x^517 + x^516 + x^515 + x^512 + x^510 + x^509 + x^507 + x^506 + x^503 + x^499 + x^498 + x^497 + x^496 + x^495 + x^493 + x^492 + x^491 + x^487 + x^483 + x^479 + x^477 + x^475 + x^473 + x^467 + x^466 + x^465 + x^464 + x^462 + x^456 + x^455 + x^454 + x^452 + x^445 + x^444 + x^442 + x^438 + x^437 + x^436 + x^435 + x^434 + x^432 + x^431 + x^430 + x^429 + x^427 + x^426 + x^425 + x^424 + x^421 + x^420 + x^419 + x^418 + x^415 + x^412 + x^409 + x^404 + x^399 + x^398 + x^397 + x^396 + x^391 + x^390 + x^389 + x^387 + x^386 + x^385 + x^384 + x^383 + x^382 + x^379 + x^377 + x^376 + x^370 + x^368 + x^366 + x^363 + x^361 + x^356 + x^355 + x^353 + x^350 + x^349 + x^345 + x^343 + x^342 + x^340 + x^339 + x^332 + x^331 + x^329 + x^328 + x^327 + x^324 + x^321 + x^320 + x^315 + x^312 + x^309 + x^308 + x^307 + x^306 + x^305 + x^304 + x^300 + x^299 + x^297 + x^296 + x^295 + x^294 + x^293 + x^292 + x^290 + x^285 + x^284 + x^278 + x^277 + x^276 + x^275 + x^273 + x^272 + x^270 + x^269 + x^268 + x^267 + x^266 + x^265 + x^262 + x^261 + x^260 + x^258 + x^257 + x^256 + x^254 + x^251 + x^250 + x^248 + x^247 + x^245 + x^244 + x^240 + x^237 + x^235 + x^234 + x^233 + x^232 + x^231 + x^229 + x^225 + x^222 + x^220 + x^219 + x^217 + x^216 + x^214 + x^213 + x^210 + x^209 + x^207 + x^203 + x^202 + x^199 + x^196 + x^192 + x^191 + x^188 + x^187 + x^185 + x^184 + x^183 + x^182 + x^174 + x^173 + x^170 + x^169 + x^168 + x^167 + x^166 + x^162 + x^158 + x^157 + x^156 + x^152 + x^150 + x^148 + x^147 + x^146 + x^144 + x^142 + x^141 + x^140 + x^138 + x^137 + x^134 + x^129 + x^128 + x^125 + x^124 + x^123 + x^122 + x^121 + x^120 + x^115 + x^113 + x^112 + x^111 + x^109 + x^108 + x^106 + x^104 + x^101 + x^100 + x^98 + x^96 + x^95 + x^94 + x^92 + x^91 + x^89 + x^87 + x^86 + x^85 + x^84 + x^77 + x^75 + x^73 + x^70 + x^68 + x^67 + x^66 + x^60 + x^57 + x^53 + x^51 + x^50 + x^49 + x^46 + x^44 + x^43 + x^42 + x^41 + x^39 + x^36 + x^35 + x^32 + x^30 + x^28 + x^27 + x^25 + x^24 + x^23 + x^20 + x^18 + x^17 + x^10 + x^9 + x^8 + x^5 + x^4 + x^3 + x^2 + x + 1

第二步

最终sage脚本：

#!/usr/bin/env sage
# coding=utf-8

from pubkey import P, n, e

R.<a> = GF(2^2049)
s = 32317006071311007300714876688669951960444102669715484032130345427524655138867890893197201411522913463688717960921898019494119559150490921095088152386448283120630877367300996091750197750389652106796057638384067568276792218642619756161838094338476168159556453601265765511288390609481762790328746654022428513989046750129115246804089185303461066541339094444328204316234109388933910370158100843030051728054627530536729824777516805905899770498822259056187070402511849965425042438274115570349075084130902413854095783358135197006242574797064057376755714941599376945465613553851989226952375198412025505190650251349584328523777

def egcd(a,b):
    if a == 0:
      return (b, 0, 1)
    else:
      g,y,x = egcd(b % a, a)
      return (g, x - (b // a) * y, y)

def modinv(a,m):
    g, x, y = egcd(a,m)
    if g != 1:
      raise Exception('Failed')
    else:
      return x % m

def getflag(d,cipher):
    c_int = Integer(cipher.encode('hex'), 16)
    c_poly = P(R.fetch_int(c_int))
    p_poly = pow(c_poly, d, n)
    p_int = R(p_poly).integer_representation()
    flag = format(p_int, '0256x').decode('hex')
    return flag
    
if __name__ == '__main__':
    d = modinv(e,s)
    with open('flag.enc', 'rb') as f:
        cipher = f.read()
    print getflag(d,cipher)

zer0lfsr

writeup：https://github.com/p4-team/ctf/tree/master/2019-03-23-0ctf-quals/crypto_lfsr

题目给了两个文件，一个是加密脚本，一个是加密结果

通过加密脚本我们可以看到flag是由三部分组成，我们的目标就是找到这三个init。刚开始看这道题目的时候，想到虽然可以知道每一次combine的结果是什么，但是要用此来推出x1、x2、x3也太多种可能了，然后就去吃饭了，后来看到z3约束求解器的存在

安装z3

1	sudo pip install z3-solver

writeup脚本如下：

# -*- coding:utf8 -*-
from libnum import n2s
from z3 import *
import hashlib

def combine(x1, x2, x3):
    return (x1 * x2) ^ (x2 * x3) ^ (x1 * x3)

def solve_3_lfsr(keystream, relevant_bit_indices, length, mask_length):
    len_mask = (2 ** (mask_length + 1) - 1)
    result_bits = map(long, "".join([bin(ord(c))[2:].zfill(8) for c in keystream]))
    s = Solver()
    x = BitVec('x', length)
    y = BitVec('y', length)
    z = BitVec('z', length)
    inits = [x, y, z]
    for result in result_bits:
        combs = []
        new_inits = []
        for index in range(3):
            relevant_bit1 = (inits[index] & (1 << relevant_bit_indices[index][0]))
            bit1_value = LShR(relevant_bit1, relevant_bit_indices[index][0])
            relevant_bit2 = inits[index] & (1 << relevant_bit_indices[index][1])
            bit2_value = LShR(relevant_bit2, relevant_bit_indices[index][1])
            single_lfsr_result = bit1_value ^ bit2_value
            combs.append(single_lfsr_result)
            new_init = ((inits[index] << 1) & len_mask) ^ single_lfsr_result
            new_inits.append(new_init)
        s.add(combine(combs[0], combs[1], combs[2]) == result)
        inits = new_inits
    s.check()
    model = s.model()
    x_res = int(str(model[x]))
    y_res = int(str(model[y]))
    z_res = int(str(model[z]))
    return x_res, y_res, z_res


with codecs.open("keystream", 'rb', 'utf8') as input_file:
    data = input_file.read()
    mask1 = (47, 22)
    mask2 = (47, 13)
    mask3 = (47, 41)
    x, y, z = solve_3_lfsr(data[:24], [mask1, mask2, mask3], 48, 48)
    init1, init2, init3 = map(n2s, [x, y, z])
    print "flag{" + hashlib.sha256(init1 + init2 + init3).hexdigest() + "}"