强网杯

Posted on

Web没什么好写的…主要记录一下rsa方面的操作

copperstudy

1
2
3
4
5
6
7
8
import hashlib
def proof(prefix,check):
    for a in range(0,256):
        for b in range(0,256):
            for c in range(0,256):
                skr = prefix + chr(a) +chr(b) + chr(c)
                if hashlib.sha256(skr).hexdigest() == check:
                    return skr.encode("hex")

第一关，已知明文m高位

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
n = 0x21b23a088ed1aadf9cfd65ccfd9002920f451be3bd25809eb926d5ee63ec3640285867836aa265843832d544a653c9107fcbee6aea10dbee68ab197c83f777f8cab7490d848bf6f93c04f255f7c4c2bff40a299af7b6651e6849cf51b7483b413c6c4a318f65cac0bdc2ddcbf35a46f84f64b6c8351eedb83004c0710d74ba67
e = 3
m = randrange(n)
c = pow(m, e, n)
beta = 1
epsilon = beta^2/7
nbits = n.nbits()
kbits = floor(nbits*(beta^2/e-epsilon))
#mbar = m & (2^nbits-2^kbits)
mbar = 0x60988a05ec4c786d06c7fa6a9f51cf180bc317ccaa693440c6415146cbe1cac5d7448a126f831f9d7ad1b985c6044f9c50d192985f3029000000000000000000
c = 0x1f067dc0bdf1ee5b2ceb213bbdea6a4ed4ed0f952d7de4eaba5ba82608b9fdd4fd06fb7e5b87894c39bff11b9d767a45fb639746dc428cd74e35a28a24005a302663817fc0d1359ef740406efdc4a84ef9320c5a03162d1f31ebc75da7994cb1431789b58c31978772363769c131e19ef649b7c70fd4ecaf4bbeb8b5bca1d461
print "upper %d bits (of %d bits) is given" % (nbits-kbits, nbits)
PR.<x> = PolynomialRing(Zmod(n))
f = (mbar + x)^e - c
x0 = f.small_roots(X=2^kbits, beta=1)[0]  # find root < 2^kbits with factor = n
realM = mbar + x0
print realM

第二关，已知高位p

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
from sage.all import *
import binascii
n = 0xa6b76d86fbe3422d7bf39f080af4f9b02123689cc3a159e45d37b4d0ba8a9bdfb2cd5aa33015ce340ddad5f1cbb83cf5c3b96608eece80f1d344dd1218da1ebcc3bfa6625b4a7fb1c46b141221e0d23cec7c4af7d9042c83c54294947ebf1a13394979fc5087b0fdc5e813048a449a1d0757fd7607e8b52347de05047b33df29
p4 = 0xb40cb1075e1112f541c2200814e43b61e2356e93e5d1bf40f8badbdd84dc10b1fe5428f4f42c022c16f6da376984405100000000000000000000000000000000
cipher = 0x5f54528ed67cac0b5a59fce6531cc850b5a65f490f3580148925b7869214ec3fc7c928379a5d770352d19c7cca3eeeb9f8bae0648c6427b4161baab3d49bff628cab0fbbabd1253769bee786903fa0ec21fa4c799ab9675ae0fbf4ac66abd30ef1796d1eb96a9c6ee56b13c39e6ed621ba8da9e5ccf44843cd44357800b5d0e8
e2 = 65537
kbits = 128  #未知需要爆破的比特位数
PR.<x> = PolynomialRing(Zmod(n))
f = x + p4
roots = f.small_roots(X=2^kbits, beta=0.4) #进行爆破
if roots:        #爆破成功，求根
    p = p4+int(roots[0])
    assert n % p == 0
    q = n/int(p)
    phin = (p-1)*(q-1)
    d = inverse_mod(e2,phin)
    flag = pow(cipher,d,n)
    print flag

第三关，e较小，已知d的低位，Partial Key Exposure Attack(部分私钥暴露攻击)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
def partial_p(p0, kbits, n):
    PR.<x> = PolynomialRing(Zmod(n))
    nbits = n.nbits()

    f = 2^kbits*x + p0
    f = f.monic()
    roots = f.small_roots(X=2^(nbits//2-kbits), beta=0.3)  # find root < 2^(nbits//2-kbits) with factor >= n^0.3
    if roots:
        x0 = roots[0]
        p = gcd(2^kbits*x0 + p0, n)
        return ZZ(p)

def find_p(d0, kbits, e, n):
    X = var('X')

    for k in xrange(1, e+1):
        results = solve_mod([e*d0*X - k*X*(n-X+1) + k*n == X], 2^kbits)
        for x in results:
            p0 = ZZ(x[0])
            p = partial_p(p0, kbits, n)
            if p:
                return p


if __name__ == '__main__':
    n = 0x359f1a3579b0feb2c8315eabd4f18300d0a436246c514c6f20315b367abdf7fa8bb2a67f463e93ee55e904709b9d8bb41961e05fab0996b021d14a41e95854b0d5fa4cd5b8bd4b5dfc239d457225a82e5193bfa9607c8a10717a33e9e50560d8448eef09f59d3174e4d574ba311cb85c22d8b2ba94bb2aa9459fa7e4556eabf5
    e = 3
    d = 0xf03a5b5181ef301c0e90d9f9f8c89321dc224848e6438132b8bbe2578335c0ce512875d46a93cc2a2afcc64d53604ac12f2b5b9520507919ca651141635cf533
    beta = 0.6
    epsilon = beta^2/7

    nbits = n.nbits()
    print nbits
    kbits = floor(nbits*(beta^2+epsilon))
    print kbits
    d0 = d & (2^kbits-1)
    print "lower %d bits (of %d bits) is given" % (kbits, nbits)

    p = find_p(d0, kbits, e, n)
    print "found p: %d" % p
    q = n//p
    print d
    print inverse_mod(e, (p-1)*(q-1))

第四关，使用不同的模数n，相同的公钥指数e加密相同的信息，广播攻击。一般会是e=k，然后给k组数据，使用中国剩余定理

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
import gmpy2
n1 = 0x4b25bd834da788533ebef06f552bc8230024d1a571226770bd93bad3b202af4de7f680252a61cc423b3143db075196d6c282e71e84a3f3fe582c69c822389ddf76a86f9169334868119a884b8185c4ee559a3540141c785f2a9e1d59e3c828b26fc785ae4b578da073a39000fbaca6f30807a6110079dc64693dd1089835ea0bL
n2 = 0x2388ddafc70ba72e181857376f3b23bf6b95c5f721a05e5e499caed0ee81a40031223718156752eef2c7535d8d8d0224126975492f8f002ca98d923ba3f05bff14eac24fb35dd50683cadc3ae0fa55ac368ebe5eb4ecfeb48ada4d785d7c64524783ef50a7c599a27b6a2afa9e1c1a41c6aba40dfd316eef4dc6718eba2af1c5L
n3 = 0x33e9cbd05b84dc1e5d314656c937c2225351bd0573a5d2d8db357db8afb65be91b0362f8c1b9bbaab51c23decfff77cf8160e260c3374c2fd5b69d1a64cdddb5bd6e37e049e4a657d4a239177b9ec23a873ae272861567b8ea000880d0ba8e7f0449de97f955a78e78e7c8a3becbf3adb6825326786d98ecc30d34be67b5be69L

e = 3
c1 = 0x5e6a4b86018060a6c38952cfd450695ca90444c51d4e0de4690dbadd5000f7bb62e752bbd70c27f342792cc669f0d650b0c8e31b233963c32ebc2297d5aae650a8be7ba5a49319cc010ea8333de09fb4ae9e25af4cce79afcaad80263fbb02329dadb49bfb5f87791c9d29e52103f0153a200f7a11b00086c3c7ae6bbc30269L
c2 = 0x71c907c67faf78314ff0332a7fe1d23fd6c9d788425affd54b851c805327fe363c340b047b555f356b1d8b6a930cb22a2e2eb3eb492ab4b307bc782c34fe1dfd032a2d838a80fbf8f6990baa4c712bc9f3bcae964806d418301cd25bc35c0d07a3fc24b25ecc527d3bfafaa5c6ffcf171446238925a76039a2aadc557efb871L
c3 = 0x37bf32f9bfd3afc668b2fb4f48ab3e888bbc204eda2dd05af8dc08974698aa7808cb8623ee16cb17ccc9e27de90d283569390f1ea155a645e46a47f4a1c147d139b631219a94ea3fcac314515a112c7e673ddf594482eec00c0ec8c46dbf4bc4532c19a5dcdbc0a1c8882937b5546653e73c047473df8aa350d876c7a62f60fL

N = n1*n2*n3
N1 = N/n1
N2 = N/n2
N3 = N/n3
u1 = gmpy2.invert(N1, n1)
u2 = gmpy2.invert(N2, n2)
u3 = gmpy2.invert(N3, n3)
M = (c1*u1*N1 + c2*u2*N2 + c3*u3*N3) % N
m = int(gmpy2.iroot(M,e)[0])
print(m)

第五关，n相同，明文相差1大部分相同，可进行 Coppersmith’s Short Pad attack和 Franklin-Reiter related messages attack

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
def short_pad_attack(c1, c2, e, n):
    PRxy.<x,y> = PolynomialRing(Zmod(n))
    PRx.<xn> = PolynomialRing(Zmod(n))
    PRZZ.<xz,yz> = PolynomialRing(Zmod(n))

    g1 = x^e - c1
    g2 = (x+y)^e - c2

    q1 = g1.change_ring(PRZZ)
    q2 = g2.change_ring(PRZZ)

    h = q2.resultant(q1)
    h = h.univariate_polynomial()
    h = h.change_ring(PRx).subs(y=xn)
    h = h.monic()

    kbits = n.nbits()//(2*e*e)
    diff = h.small_roots(X=2^kbits, beta=0.5)[0]  # find root < 2^kbits with factor >= n^0.5
    return diff

def related_message_attack(c1, c2, diff, e, n):
    PRx.<x> = PolynomialRing(Zmod(n))
    g1 = x^e - c1
    g2 = (x+diff)^e - c2

    def gcd(g1, g2):
        while g2:
            g1, g2 = g2, g1 % g2
        return g1.monic()
    return -gcd(g1, g2)[0]

if __name__ == '__main__':
    n = 0x198f61bc7d2977139120b86b739afbd04e82726a7dcf514cc2ad46c7002d2202915ba932364d71b7dd1928fb6861f984d8d9e31e70d0023aca721130e1df2825568a623c8316fd555616d91897a2db5d1df973a1584ed4cfb0f55d910db5ff64a79f061ef71b2362b6c2af8416a5a47094aff428d6c541448df45436ec48f93
    e = 3

    nbits = n.nbits()
    kbits = nbits//(2*e*e)
    print "upper %d bits (of %d bits) is same" % (nbits-kbits, nbits)

    # ^^ = bit-wise XOR
    # http://doc.sagemath.org/html/en/faq/faq-usage.html#how-do-i-use-the-bitwise-xor-operator-in-sage
    
    c1 = 0x13a5213f8946b3da1b37a7346f7985ed17329b05c31cc72912e15ab62c2b578f95148f7f2fb3daed063f5517efd9694d8a87792b675715d50d9113baa0bbfb1791f8e551ce5583c3dc31adf37dced9dab4acf3e58a5f3e203b1c971a746de5e9ac0b4d0153538f9392a0ce12250c5597eb23f07b4d7c84a084fc1dd0dee6b1c
    c2 = 0xa864c9ffa08edc2d2a380fde218fe07204193c43580ee0a3fd1505e3f60125c3f380fab24bbd344bca174f3b5b09ed271b817cb08fa6087f2b9d2216a1c7782714c50f475b0e3ca8b530ae33f4f4fb72c14ac0331b107d9dfcbbb193ac6946edd01e9cf5cab799a444dd9a49eb5362f6a499fa69540ac1d3dfbb977f57cd8e

    diff = short_pad_attack(c1, c2, e, n)
    print "difference of two messages is %d" % diff

    m1 = related_message_attack(c1, c2, diff, e, n)
    m2 = m1 + diff
    print "m1 is %d" % m1
    print "m2 is %d" % m2

第六关，知道n、e、c，并且e很大，Boneh and Durfee attack

我们知道，如果要使用Wiener’s Attack，则d要满足以下条件

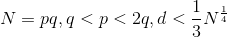
那如果e很大，但是d比上述要大，那就可以尝试Boneh and Durfee attack，条件为

1
d < N^0.292

使用以下这个脚本就可以求出d

https://github.com/Gao-Chuan/RSA-and-LLL-attacks/blob/master/boneh_durfee.sage

强网先锋_辅助

知道n1、n2、c1、c2、e，q不变，因此通过求n1、n2的公约数得到q，从而得到p1，进而得到flag

1
2
3
4
5
6
7
8
9
10
11
12
13
import gmpy2
import binascii
n1 = 14967030059975114950295399874185047053736587880127990542035765201425779342430662517765063258784685868107066789475747180244711352646469776732938544641583842313791872986357504462184924075227433498631423289187988351475666785190854210389587594975456064984611990461126684301086241532915267311675164190213474245311019623654865937851653532870965423474555348239858021551589650169602439423841160698793338115204238140085738680883313433574060243600028500600824624358473403059597593891412179399165813622512901263380299561019624741488779367019389775786547292065352885007224239581776975892385364446446185642939137287519945974807727
n2 = 14624662628725820618622370803948630854094687814338334827462870357582795291844925274690253604919535785934208081825425541536057550227048399837243392490762167733083030368221240764693694321150104306044125934201699430146970466657410999261630825931178731857267599750324918610790098952520113593130245010530961350592735239454337631927669542026935873535964487595433984902529960726655481696404006628917922241666148082741874033756970724357470539589848548704573091633917869387239324447730587545472564561496724882799495186768858324490838169123077051890332313671220385830444331578674338014080959653201802476516237464651809255679979
e = 65537
c1 = 2482083893746618248544426737023750400124543452082436334398504986023501710639402060949106693279462896968839029712099336235976221571564642900240827774719199533124053953157919850838214021934907480633441577316263853011232518392904983028052155862154264401108124968404098823946691811798952747194237290581323868666637357604693015079007555594974245559555518819140844020498487432684946922741232053249894575417796067090655122702306134848220257943297645461477488086804856018323986796999103385565540496534422406390355987976815450744535949785073009043007159496929187184338592859040917546122343981520508220332785862546608841127597
c2 = 3829060039572042737496679186881067950328956133163629908872348108160129550437697677150599483923925798224328175594483217938833520220087230303470138525970468915511111320396185482564783975435346354440035776909781158407636044986403819840648379609630039348895415045723208843631191252142600667607807479954194447237061080618370787672720344741413537975922184859333432197766580150534457001196765621678659952108010596273244230812327182786329760844037149719587269632133595149294067490955644893402708720284179715002149224068928828656515326446881791228638008572889331511945042911372915003805505412099102954073299010951896955362470
q = gmpy2.gcd(n1,n2)
p1 = n1//q
phi1 = (p1-1)*(q-1)
d1 = gmpy2.invert(e,phi1)
m1 = pow(c1,d1,n1)
print(binascii.a2b_hex(hex(m1)[2:]))